Debian Cosillas: Firma y Cifrado de correos en Thunderbird

Esta última semana he disfrutado como un mono gibraltareño robándole la comida a un turista despistado. Una vez liberada DMDc 2.0, tocaba instalarla y ponerla a mi gusto. De instalarla se ocupó mi hijo de 12 años….. Imaginaos la dificultad…. De ponerla a mi gusto…. Bueno, ya sabéis, sobre gustos no hay nada escrito…. A mí me gusta el ajo crudo y mi mujer me odia por ello….

En este post voy a tratar de explicaros el uso de un complemento de Thunderbird (Enigmail) que permite el cifrado de los correos electrónicos, “asegurando” una comunicación de datos “inviolable”

Nótese el uso de comillas en las palabras “asegurando” e “inviolable”. Hoy por hoy, nada es 100x100 seguro. Todos tenemos en la cabeza el reciente caso Snowden y las escuchas de la NSA. Pero por ponérselo difícil que no quede….

Para empezar, ¿sabemos lo que quiere decir “cifrar”? También se conoce como encriptar. El encriptado consiste en transformar un texto “legible” (texto plano o plain text), en un chorizo ininteligible de datos (texto cifrado o ciphertext). Este ciphertext se genera aplicando al plain text unos algoritmos y una clave de cifrado. Posteriormente, este texto cifrado deberá ser descifrado aplicando una clave de descifrado, que puede ser igual, o no, a la de cifrado. Aquí está el meollo de la cuestión. En las dichosas claves.

Para que este proceso sea funcional, las claves de cifrado y/o descifrado deben ser seguras. Y entenderme bien, cuando digo seguras, me refiero a que no pueden conocerlas hasta la vecina del quinto, ¿ok?. El uso de métodos criptográficos se aplica al intercambio de información en un canal inseguro. En cristiano: Si yo le digo a Frannoe al oído, en una habitación cerrada, sin ventanas, aislada acústicamente y libre de escuchas, que su distro va de fábula….. ¿para que coj… quiero encriptarlo, diciéndole que las mariposas son hermosas….? ¿Os imagináis la cara de Frannoe si además no sabe que le estoy hablando en clave?

Así pues, partimos del escenario en el que tenemos un mensaje privado, que no queremos que se conozca, lanzado al exterior a través de una línea de comunicación insegura (aka Internet). Así que le aplicamos un proceso de cifrado. Este proceso consiste en aplicar al mensaje un conjunto de operaciones matemáticas (algoritmos) y una clave de cifrado. Esto es más viejo que andar p’alante. Y prueba de ello es el ilustre Julio César.

Dicho romano ideó un sistema de comunicación segura para mandar mensajes a sus generales. Este consistía en desplazar las letras del alfabeto tres espacios. Es decir, si quería escribir:

ATACAR AL ALBA

desplazaba las letras del alfabeto tres espacios a la derecha, quedando el mensaje:

DWDFDU DO DOED

Como véis, muy simple. Este sería el código:

ABCDEFGHIJKLMNOPQRSTUVWXYZ
DEFGHIJKLMNOPQRSTUVWXYZABC

¿Simple?…Pues si......pero le dió resultado….

Estamos en el año 50 antes de Jesucristo. Toda la Galia esta ocupada por los romanos… ¿Toda? ¡No! Una aldea poblada por irreductibles galos resiste todavía y siempre al invasor….

Ups!, que me voy por las ramas....

Volviendo a César. Dicho método de encriptación dió lugar al conocido como cifrado César, que también ha sido llamado cifrado por desplazamiento, código de César o desplazamiento de César. Hoy en día no tiene aplicación práctica ninguna, ya que es fácilmente descifrable, pero ha sido utilizado largamente en la historia.

Descifrar o romper un método de encriptación (llamado criptoanalizar), consiste en obtener el texto llano original a partir del texto cifrado sin conocer la clave. En el caso del cifrado César, es sencillo. Sólo tenemos que probar 25 combinaciones de letras. Es evidente que con la capacidad de procesamiento de las máquinas actuales, se tarda más en leer el texto ya descifrado que descifrarlo en sí.

Hacerlo a mano es más tedioso, pero igualmente factible. Aplicando por ejemplo el análisis de frecuencia, sabemos que las letras que más se repiten en el castellano son la E y la A. Si nos encontramos un mensaje en el que nos citan en la ciudad FDIDUQDXP, vemos que la letra que más se repite es la D. Si suponemos que la D es en realidad una E, esto significa que el desplazamiento es de 1 a la derecha. Si desciframos moviendo 1 a la izquierda, nos da: ECHCTPCWO…. Vaya, pues no sé…. La geografía se me daba bien, pero no sé si este pueblo existe o no…. ¿quizás saliendo todo recto de Reikjavik y girando al Este?... No sé. Probamos con la A. Esto supone un desplazamiento de 3 a la derecha. Descifrando con 3 a la izquierda nos da CAFARNAUM…. Eso si. Bonita ciudad…. Lógicamente, cuanto más texto cifrado tengamos, más fácilmente descifrable es el mismo, hablando del método César.

Todos estos algoritmos se fueron complicando en el tiempo, pero siempre teniendo en cuenta que para cifrar y para descifrar, se utilizaba la misma clave. A este método de cifrado se le llama cifrado simétrico. Los algoritmos más utilizados (aún hoy en día) son DES y AES. No voy a entrar a describirlos.

La desventaja del cifrado simétrico es obvia. Ambos interlocutores de la comunicación deben conocer la clave. Entonces, si el canal de comunicación no es seguro, ¿cómo le hago llegar a Frannoe la clave para descifrar mis mensajes? ¿Me voy a la habitación insonorizada de antes para decírsela? Pues ya que estoy allí, le digo lo que le tenga que decir y basta, ¿no?. Hombre, me sirve para los siguientes mensajes, que a mí viajar me da mucha pereza…

Así que para resolver este entuerto, allá por los 70 se inventó el cifrado asimétrico o de clave pública. Básicamente consiste en dos claves: una clave pública y otra privada. Utilizando el cifrado asimétrico, podemos cifrar un mensaje con la clave pública de nuestro interlocutor, ya que sólamente será descifrada con la clave privada del mismo, que ya se guardará muy bien él de tenerla asegurada a buen recaudo, y no pegada con un post-it en el monitor.

Evidentemente, esta clave pública podemos dársela a tanta gente como queramos. Es como dar el número de teléfono. Si te llaman, sólamente tú puedes descolgar el mismo. Bueno, esto no es así necesariamente, pero imaginemos que la CIA no ha pinchado nuestra línea y tiene a unos informáticos obesos con acné y melena pringosa, ocultos en un sótano descolgando tu teléfono y haciéndose pasar por tí…

Que paranoicos sois… Eso sólo pasa en las películas… Hoy en día los informáticos, aunque tengamos el pelo largo, lo tratamos con esencia de aloe vera, tenemos el cutis finísimo como el culito de un bebé, los músculos trabajados a base de gimnasio y estamos en una playa de Barbados, con un mojito fresquito debajo de una palmera…

Volviendo a la cruda realidad…. El uso de este método de encriptación es el más extendido. Tiene como uno de sus inconvenientes la velocidad de cifrado/descifrado, que es bastante más lenta que el cifrado simétrico. El algoritmo de cifrado asimétrico más utilizado el el llamado RSA (Rivest-Shamir-Adleman). Estos tres tipos son unos cerebritos del MIT (como los de Big Bang Theory, supongo), que inventaron en 1977 este algoritmo. El algoritmo es realmente simple, pero efectivo. En este sí me voy a detener, para saber cómo funciona. Os lo describo:

1.- Seleccionamos dos números primos muy grandes (del orden de 2048 bits en binario): A y B
Estos números primos son generados basándose en el generador de números aleatorios del Kernel. ¿Entendéis ahora la polémica de hace unos meses de la función RdRand de Intel? Si es predecible, no es aleatorio, así que se puede descubrir…

2.- Seleccionamos otro número ( C ) que cumpla las siguientes condiciones:
* Mayor que 1 -> C>1
* Menor que el producto de A*B -> C<(A*B)

* Tanto C, como la operación (A-1)*(B-1), tienen que tener de máximo común divisor 1

Este número se haya con la función φ de Euler.

3.- Ahora hallamos un número D que cumpla la siguiente condición:
* (D*C-1) sea divisible por (A-1)*(B-1), osea, que sea una división entera.

Este número suele calcularse mediante el algoritmo de Euclides extendido.

4.- Con todos estos números (A, B, C y D) generamos las funciones de cifrado y descifrado de la siguiente manera:

- FUNCIÓN DE CIFRADO: MC=(MO exp C) mod A*B

- FUNCIÓN DE DESCIFRADO: MO=(MC exp D) mod A*B

MO es el mensaje original como número entero positivo.

MC es el mensaje cifrado .
mod es una función que da el residuo (resto) de una división entera. 8 mod 3 es igual a 2, que es el resto de dividir 8 entre 3.

[Frannoe dixit]

Oye.... estoooo.... ¿con la Casio de mi niña se puede hacer esto?...

[Jose respondere]

No te preocupes, lo hará el sistema por tí... Pero ya verás lo que tarda...

La clave pública sería el par (A*B,C) y la clave privada el par (A*B, D). La clave pública se puede dar sin problema, ya que no es factible calcular D (clave privada) conociendo A*B y C. Quiero decir que para calcular D, es necesario conocer A y B por separado. Como lo que conocemos es el producto A*B, aritméticamente sería posible descubrir A y B, pero como éstos son números muy grandes, del orden de 2048 bits, a cualquier máquina le llevaría cientos, miles, millones de años, factorizar dicho producto. Recordar que factorizar un número, producto de dos números primos, es descubrir dichos números primos sabiendo sólo su producto.

Para que os hagáis una idea, en factorizar un RSA-640 (un bonito número de 193 cifras ó 640 bits) se tardaron varios meses (cinco, en concreto) utilizando el poder combinado de 30 procesadores Opteron. Tener en cuenta que el tiempo de factorización es exponencial, así que un RSA-1024 eleva exponencialmente su tiempo de factorización. Hoy en día, la clave que genera GnuPGP es RSA-2048. Y podríamos trabajar incluso con claves RSA-4096... Si os animáis, existe una competición de factorización RSA. El pŕoximo RSA a factorizar es RSA-704, un precioso numerajo de 232 cifras ó 704 bits. Animo, tiene un premio de 30.000 dólares….

Por último, y ya termino con este rollo, debéis saber que existe el método híbrido de criptografía, en el que encriptamos utilizando el método simétrico (más rápido), y compartimos la clave de encriptado utilizando el método asimétrico (más seguro).

[Frannoe dixit]

Uauuuu!!!!!... Entonces con esto estamos totalmente seguros, ¿no?

[Jose respondere]

NO. Ya en 1993, otro fumao del MIT, un tal Peter Shor, ideó un algoritmo cuántico (¡¡¡toma ya!!!) capaz de descomponer en factores (factorizar) un número, en un tiempo que es determinado por el logaritmo de dicho número al cubo. En cristiano:

Tipo de RSA	Tiempo de factorización con algoritmo clásico	Tiempo de factorización con algoritmo de Shor
512	4 dias	34 segundos
1024	100.000 años	4,5 minutos
2048	100.000 billones de años	36 minutos
4098	100.000 billones de cuatrillones de años	4,8 horas

Cierto, hay que construir máquinas cuánticas para ello, pero ….. ya estan aquiiiiii……..

Si alguien se ha perdido por el camino, lamento decirle que no sé explicarlo más claro.

Muchos de vosotros pensaréis que eso de utilizar claves públicas/privadas ó simétricas/asimétricas, sólo es utilizado por gurús informáticos, espías y paranoicos de la teoría de la conspiración…. Craso error. Todos aquellos que hacéis uso de repositorios en Linux estáis haciendo uso de claves públicas. Me explico.

Como sabéis, Frannoe tiene publicado en Internet un Repositorio propio para su distro DMDc. Sabéis que nos bajamos los paquetes actualizados que Frannoe y algún otro van colocando en él, para tener nuestro sistema lo más actualizado posible. Bien, pero…. ¿Cómo sabemos que los paquetes que nos bajamos del Repositorio son en realidad de Frannoe, o si son en realidad de ese Repositorio, y no de otro?

Pues haciendo uso de la clave pública de Frannoe. Si miráis los orígenes de Software (sudo software-properties-gtk, pestaña Autentificación), veréis que allí aparece una clave tal que así:

Ese numerito 81602690 es en un código que identifica la clave pública de Frannoe. En este caso, la utilizamos para verificar que los paquetes que nos bajamos de su Repositorio son en realidad hechos o subidos por él al mismo. Si tuviéramos acceso al ordenador de Frannoe, veríamos que él tiene dos claves para el mismo número. Es decir, tiene la clave pública (que ha compartido con el mundo mundial al publicarla en su Repositorio), y otra clave privada, que debería tener él y solamente él en su máquina. Esta otra clave es la que utiliza para firmar los paquetes que sube al Repositorio. De no ser así, cualquiera podría subir paquetes a su Repositorio (o a cualquier otro Repositorio). Como véis, la utilización de las claves públicas/privadas está a la orden del día.

Bueno, llegados a este punto, todo aquél que haya sobrevivido a este tostón tiene la oportunidad de ver cómo instalar este sistema en su equipo. El software necesario para generar las claves ya viene instalado en nuestro sistema, y es el paquete gnupg. Existe en los repositorios de Debian una versión más moderna, gnupg2, pero no es necesario instalarla. Nos basta con la que viene ya instalada. Como siempre que os hablo de instalar software, me refiero a software libre.

GnuPG es la implementación libre de PGP (Pretty Good Privacy), software desarrollado para encriptación de datos, en el que ha basado la Internet Engineering Task Force el estándar de internet OpenPGP (no me he podido resistir a copiarlo de la Wiki….. Es que suena tan bien y queda tan profesional…..)

En fín, que ya está instalado. Para utilizarlo en Thunderbird, tendremos que hacer el complicado paso de…. instalar un Add-on. Si no sabéis instalar un complemento en Thunderbird, es tan difícil como pulsar el menú, acceder a Complementos, y una vez abierta la pestaña de los mismos, escribir en el cuadro de búsqueda: Enigmail, y proceder a instalarlo.

Una vez instalado, os indicará que hasta que no se reinicie Thunderbird, no estará disponible….. Complicadillo, ¿eh?

Bien, pues vamos ahora con la clave, el meollo de la cuestión. Para aquellos que odian profundamente la consola, Enigmail ha tenido a bien generar un asistente de configuración que se abrirá nada más iniciar de nuevo Thunderbird. Aquellos despistados que lo cierren, pueden acceder al mismo desde el menú:

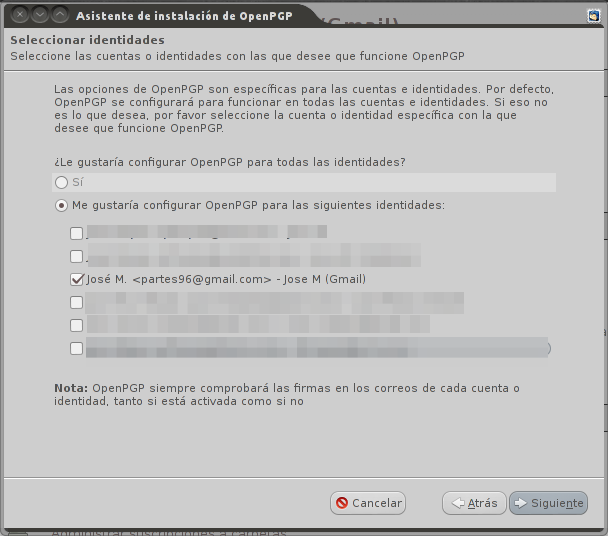
Si tenemos varias cuentas configuradas, lo primero que nos preguntará es si queremos configurar OpenPGP para todas ellas. Oye, a gusto del consumidor:

Ahora nos preguntará si deseamos firmar todos los mensajes salientes. Lo mejor en este caso es hacerle caso, y dejar pulsada la opción de firmar todos los mensajes salientes. A más de uno le sorprenderá recibir un correo vuestro firmado digitalmente, y a buen seguro se pondrá en contacto con vosotros para preguntar de qué va eso…. Aprovechar, demostrarles que sois expertos en seguridad informática…. o marcar la otra opción, y crear reglas para firmar selectivamente a vuestros destinatarios. Repito, a gusto del consumidor.

Bien, la siguiente preguntita sí es importante (no es que las anteriores no lo sean). Vamos a ver. Si seleccionamos cifrar todos los mensajes salientes, debemos tener las claves públicas de todos nuestros destinatarios. En la vida real, eso es imposible. ¿Y si mañana tienes que enviar un correo a una tienda on-line, por ejemplo? ¿Te pones en contacto con ellos y les dices que te envíen su clave pública? A más de uno os van a enviar a coger amapolas, os advierto…

La siguiente pregunta del asistente realizará una serie de cambios en el funcionamiento del Thunderbird, que, como bien explica, no notaréis. Dejamos marcado SI.

Uno de los cambios que realizará, es que los mensajes se enviarán en modo texto simple, o lo que es lo mismo, deshabilitará el envío de mensajes en formato HTML. Si no lo hiciéramos así, nos saldrían advertencias como esta:

Continuamos. Como decía anteriormente, para aquellos temerosos de la “infernal” consola, el asistente nos propone crear un nuevo par de claves para firmar y cifrar, evitando el crearlas a mano desde la consola. Aquellos que ya tengáis vuestras claves creadas, podéis optar por importarlas.

La siguiente pantalla no tiene desperdicio. Vamos a detenernos un poco, leyendo lo siguiente:

TOMA, TOMA y TOMA…. ¿Quién dijo que la informática es aburrida? Un par de claves tiene dos claves….. Juas, juas, juas….. Sí señor, con un par de…. claves. Ayyyy, señor….

Una vez pasado este interludio jocoso, observamos que nos pide una contraseña. No os confundáis, no está pidiendo la contraseña de la cuenta de correo, os está pidiendo que le pongáis una contraseña a vuestra clave privada. No hace falta que os hable de la seguridad de las contraseñas, ¿verdad?. Olvidaros de “12345678”, “password”, “sex”, etc…

Y un resumen para finalizar

Ea, pues dejarlo trabajar, que para eso está construido...

De la "fuente de aleatoriedad" o "piscina de entropía" os hablaré otro día. Saber sólo que la generación de esta clave tardará menos si se llena, así que hacerle caso y abrir caja, o navegar por Internet un ratito.

Al finalizar, nos recomienda firmemente crear un certificado de revocación para nuestra clave. Ya que estamos, le decimos que sí. No vamos a llevarle la contraria por sistema…

Simplemente, escogemos un nombre para el certificado de revocación. Tener en cuenta de no dejarlo en un directorio compartido ni nada por el estilo.

Para comprobar que todo está bien, nos pìde la contraseña de la clave privada creada:

Bien, pues ya puestos, vamos a aprender a usarlo. Recordar que hemos marcado firmar todos los correos salientes y cifrar sólo aquellos que deseemos. Vamos a ver cómo actuaríamos con Frannoe, aunque las pruebas las haré con dos cuentas mías en dos ordenadores distintos.

Empezamos. Importante recordar, de todo el rollo que os solté al principio, que si quiero cifrar un correo a Frannoe, necesito hacerlo con su clave pública. Luego él, con su clave privada lo descifrará. Y si él me quiere contestar de manera cifrada, necesita tener mi clave pública, y luego yo lo descifraré con mi clave privada. Así que sin prisa pero sin pausa, procedo a enviarle un mensaje a Frannoe.

Una vez escrito, antes de enviarlo, selecciono el menú OpenPGP. Vemos que por defecto está activa la opción de Firmar mensaje. Necesitamos marcar Adjuntar mi clave pública.

Bien, ya le he enviado mi clave privada a Frannoe. Ahora él, que ya estaba avisado y había hecho los pasos anteriores en su máquina, al recibir mi mensaje, le aparecerá un archivo adjunto con la extensión “asc”, que es mi clave pública. Guardará el archivo, y desde el menu OpenPGP seleccionará Administración de claves, para proceder a importar el archivo.

En este mismo momento, podemos elegir si añadimos dicha clave a una regla por destinatario o dejarla importada sin más. En este último caso, una vez que deseemos enviar un mensaje cifrado, nos pedirá seleccionar con qué clave de las que tenemos almacenadas deseamos cifrarlo.

Bien, ya le he enviado mi clave a Frannoe. A su vez, Frannoe, aunque no siempre hace lo que le pido, ha sido condescendiente con mi petición y me ha enviado su clave pública. Y yo, que no voy a ser menos que él, procedo a importarla en mi sistema de la misma forma.

Pues ya está hecho. Ahora Frannoe me enviará un correo, seleccionando en el menú OpenPGP la opción Cifrar Mensaje.